Introduction

There is an old saying that says, "too many cooks, spoil the broth." In this web page the inverse is introduced, that is "many bad cooks, make good soup."

From simple mathematics, we know that negating a negative number produces a positive number. In a game of chess, you might sacrifice pieces in order to win the overall game. But, can two losing games be set up to produce a winning scenario? The answer is yes. This counterintuitive behaviour is called "Parrondo's Paradox."

Parrondo's games were devised by the Spanish physicist Juan M. R. Parrondo in 1996 and they were presented in unpublished form at a workshop in Torino, Italy. After about three years, in 1999, Harmer and Abbott published the seminal paper on the games, naming them after Parrondo who's genius inspired them.

The main idea of Parrondo's paradox is that two individually losing games can be combined to win via deterministic or non-deterministic mixing of the games. There has been a lot of research on Parrondo's games after the first published paper, giving birth to new games such as history-dependent games (instead of capital-dependent) and cooperative games (multi-player games instead of one player).

Some workers have criticized the use of the term “paradox”—however we use it in the sense of an apparent paradox and this is comparable to existing terminology, such as in “Simpson’s paradox," the “Braess paradox” and the "renewal paradox."

Original Parrondo's games (capital dependent)

The original Parrondo's games are made up of two games, namely Game A and Game B. The definition of both Games A and B are as follows. At each discrete-time step n, either Game A or B will be played. The algorithm or pattern utilised to decide which game to be played at each discrete-time step n is defined as the switching strategy.

Game A consists of a biased coin that has a probability p of winning,

Game B consists of 2 sub-games, the condition of choosing either one of the games is given as below:

C divisible by M, play a biased coin that has probability p1 of winning,
Otherwise, play a biased coin that has probability p2 of winning.

When Game A and Game B are played individually, they will lose definitely. The paradox appears when Game A and Game B are mixed and played together by a "switching strategy" rule.The switching strategy used can be random or periodic. Another switching strategy that can be used to give "Parrondo's paradox" is chaotic switching. With chaotic switching, the rate of winning of Parrondo's games is found to be higher that one achieved by random switching. However, periodic switching still give the highest rate of winning since a periodic switching favours the occurance of the game with higher winning probability in Game B.

History Dependent Parrondo's games

Another breakthrough by Juan M.R. Parrondo is the creation of new paradoxical games, which are based on history of the games. If the player wins a game at discrete unit step time (n), his state will be assigned to "win", otherwise to "lose". The states of the player at each discrete unit step time are recorded as a history of the games.

The parameter space for the appearance of Parrondo's paradox with history dependent games is wider than one with modulo capital dependent games. Hence, the creation of history dependent games possibly opens up wider application areas of Parrondo's paradox.

In the history dependent games, Game A remains unchanged as defined in capital dependent games. The only difference is the structure of Game B. Game B is made up of four sub-games where the decision on which sub-game to be played at each round (or discrete unit step time) is based on the history of games. This can be clearly shown as below:

Cooperative Parrondo's games

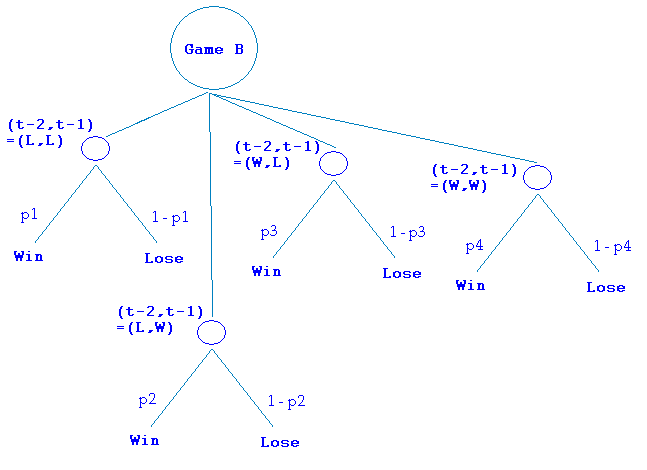
Inspired by history dependent games, Toral devised another new family of Parrondo's games called "cooperative Parrondo games." Instead of having one player to play with the banker (banker is defined as one who makes the payoff for a player who wins and takes the payoff from a player who loses), we have multiple players, say from i = 1, 2, ..., N. Assume that all the players form a "ring" such that player N is sitting between player N - 1 and player 1, and so on.

On each round, only one player will play the games. So, each player will wait for his turn to play the games, or a random selection of players can be carried out. If a player wins a game, his state will be assigned to "win," otherwise assigned with "lose." A player keeps his state until his next round of game is played.

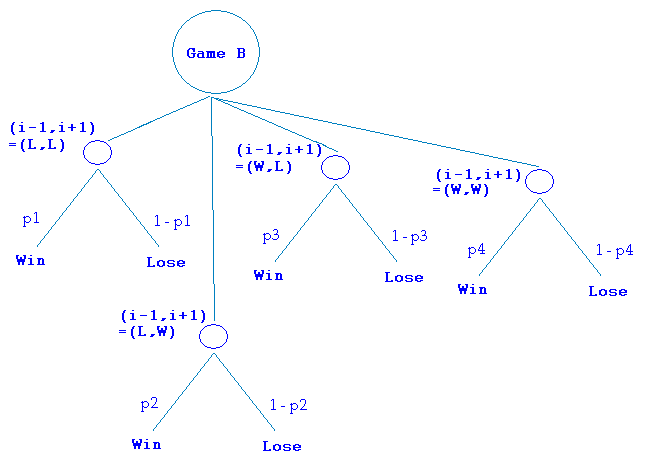
Similar to history dependent games, Game A remains unchanged as defined in the original Parrondo's games. The structure of Game B in cooperative Parrondo's games is similar to one in history dependent games but not exactly the same. There are also four sub-games that makes up Game B, but the decision on which sub-game to be played at each round of player i is based on the state of two neighbour players, i - 1 and i + 1.

Relationship between Brownian ratchet and Parrondo's games

Copyright © The University of Adelaide 2003 Last Modified Derek
Copyright | Privacy | Disclaimer